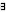  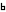 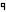 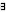    
|
09 年03 月 06 日: 「1=2」 ---15:48:54 add
アンサイクロペディアで
「1=2」
が真であることの証明を見てたら頭痛くなってきた。
a = 1
b = 1 のとき
両辺に a を足して
a + b = 2a
両辺から 2b を引いて
a − b = 2a − 2b
(a − b) = 2(a − b)
両辺を (a − b) で割って
1 = 2
うおっ証明されとるやん!世の中の法則面目丸つぶれ!と数秒思いつつ。
回答は「続き」より
元々遭遇したのが「0で割る方法」だったので逆に分からなくなってきてましたが、「両辺を(a-b)で割る」っていうのがNGでしたね。
a=bが前提なのでx/(a-b)はゼロ除算になってしまうということで。方程式を使われたことで逆に気付きが遅れてしまったな。「0で割れる事の証明」の前提が「0で割れる事が真である」というのもなんか笑える。wikipediaの方を見ると逆にこの方法が「ゼロ除算が出来ないことの証明」として説明されているのもまたなんとも趣深し。
いやしかしこういうウィットを装った(良い意味で)悪質な冗談ってのは面白いなぁ。もっと先にでてる「余り」を使う方法とか秀逸過ぎるだろw
「メダカの王国」でネタにされていた
・仕掛け人を含む参加者3人がそれぞれ1000円ずつだして場に3000円を提示する。
・参加者に「この3000円を2500円で買うヤツは居ないか」と募る
・バカ「A」が騙されて「買う買う!」と2500円を仕掛け人に支払う
・「A」以外の参加者にに1000円をそれぞれ返却する
・「A」に3000円渡す
・余った500円を仕掛け人がふんだくる
とかふつーに冷静に考えればすぐ気がつくんだけど、ああいう勢いで遣られると俺も騙されそう。2500円を受け取ってから「支払い」するまでを迅速かつナチュラルに実行することがキモだな。
パタリロに出てきた「おつりをちょろまかす店員」もまた然り。
